この記事の内容
先日「射影行列の導出」という記事を作成しました。
その中で「射影行列 \(P\) 」がランク落ちしているということに言及しました。記事の中では、その説明はしていなかったのでこの記事でその補足をしようと思います。
また、前回の記事の結果から分かる「射影行列の設計」に関しても少し触れたいと思います。
\(P \) がランク落ちしていることの説明
以前の記事の中でも触れているのですが、 \( P^2 = P\) という条件だけから \( P \) がランク落ちしていることが分かります。
では、早速その説明に入っていきましょう。
準備
行列 \( P \) について、表記の仕方を以下の二通りとします。
$$ P = \left[ \begin{array}{cccc} p_{1} & p_{2} & \dots & p_{n} \\ \end{array} \right]$$
$$ P = \left[ \begin{array}{cccc} q_{1}^{T} \\ q_{2}^{T} \\ \vdots \\ q_{n}^{T} \\ \end{array} \right]$$
\(p_{i}\) \( (i=1,2, \dots, n) \) は列ベクトル、\(q_{i}^{T}\) \( (i=1,2, \dots, n) \) は横ベクトルです。
この表記をベースに、次節で述べる方針に基づいて \(P\) のランク落ちを導きます。
方針
\( P^{2} = P \) をあるベクトル \( v \in {\bf R}^{n} \) に左から掛け、それを式変形することで
$$ \sum_{i = 1}^{n} c_{i} p_{i} = 0 $$
という形を導きます( \( c_{i} \) は定数 )。これは「\( P \) の列ベクトルが線形従属」であることを意味し、それはすなわち \( P \) がランク落ちしていることと等価です。
証明
\( v = v \) という式の左から、 \( P^{2} \) と \( P \) をそれぞれ掛けると、以下の等式が成り立ちます。
$$ P^{2} v = P v \tag{1}$$
\( P^2 \) については次のように変形できます。
$$ P^{2} = \left[ \begin{array}{cccc} p_{1} & p_{2} & \dots & p_{n} \\ \end{array} \right] \left[ \begin{array}{cccc} q_{1}^{T} \\ q_{2}^{T} \\ \vdots \\ q_{n}^{T} \\ \end{array} \right]$$
$$ \Leftrightarrow P^{2} = \sum_{i=1}^{n} p_{i} q_{i}^{T} $$
これより、(1)式の左辺は以下のように表すことができます。
$$ P^{2} v = \sum_{i=1}^{n} p_{i} q_{i}^{T} v = \sum_{i=1}^{n} (q_{i}^{T} v) p_{i} = \sum_{i = 1}^{n} a_{i} p_{i} \tag{2}$$
ただし、 \( a_{i} = q_{i}^{T}v \) はスカラーの定数です。
(2)式の内容を(1)式に反映し、変形すると以下のようになります。
$$ \sum_{i = 1}^{n} a_{i} p_{i} = Pv = \sum_{i = 1}^{n} v_{i} p_{i} $$
$$ \Leftrightarrow \sum_{i = 1}^{n} (a_{i} – v_{i}) p_{i} = 0 \tag{3}$$
\( a_{i} – v_{i} \) を改めて \( c_{i} \) を置くと、\( \sum_{i = 1}^{n} c_{i} p_{i} = 0 \) という形の式が導かれたことが分かります。したがって、ゼロではない定数 \( c_{i} (i=1,2,\dots n)\) が存在して、前述の式が成り立つので \( p_{1}, p_{2}, \dots p_{n} \) は線形従属となります。したがって、\( P \) はランク落ちしていると言えます。
余談ですが、\( P \) がランク落ちしているということは、 \( {\rm Ker} P \) の次元が1以上であることを意味します。つまり、任意の数ベクトルを \( P \) によって線形変換すると、その像の次元が少なくとも1は落ちるということになります。射影の直感的な意味とも符合することが分かりますね。
射影行列の設計について
先日の記事でも紹介したように、「\( {\rm Ker} B^{T} \) に沿った \( {\rm Im}A \) への射影 \( P \) 」は以下の式で表現できます。
$$ P = A (B^{T} A)^{-1} B^{T} $$
\( A \) は射影先の部分空間の基底ベクトルを列ベクトルとして並べた行列であり、 \( B \) は射影方向を表す空間の直交補空間の基底ベクトルを列ベクトルとして並べた行列でした。
すなわち、
- 射影を考える空間の次元
- 射影先の部分空間の基底ベクトル
- 射影方向に該当する空間の直交補空間を構成する基底ベクトル
の3要素が決まれば、射影行列は一意に決められるということです。少し例を用いて説明してみようと思います。
簡単のために2次元空間を考えます。
問題としては、任意の二次元ベクトル\( (x’, y’) \) を、\( y = -2x \) に沿って、\( y =x \) 上に射影する、というものを考えます。イメージは以下の図のようになります。
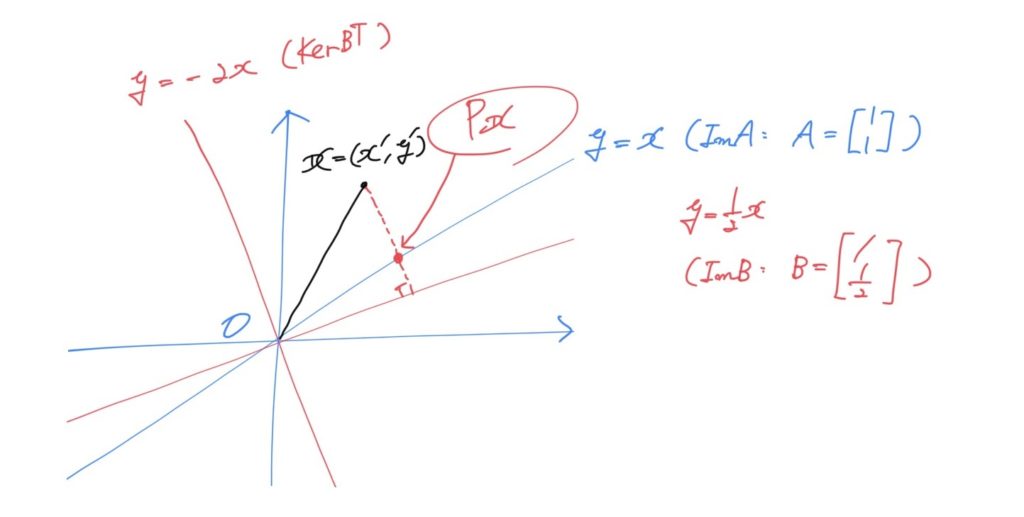
この例において、射影先の空間 \( {\rm Im} A \) の基底ベクトル、射影方向の直交補空間 \( {\rm Im} B \) の基底ベクトルはそれぞれ以下のようになります。
$$ A = \left[ \begin{array}{c} 1 \\ 1 \end{array} \right] $$
$$ B = \left[ \begin{array}{c} 2 \\ 1 \end{array} \right] $$
ぱっと思いつくベクトルを用意しているので、単位ベクトルでないことに注意してください。
※ 実は、基底ベクトルのノルムには縛りがなく、どんなものでも機械的に射影行列が求まります。
これに基づいて射影行列 \( P \) を求めると、以下のようになります。
$$ P = A (B^{T}A)^{-1} B^{T} = \left[ \begin{array}{c} 1 \\1 \end{array} \right] (3)^{-1} [2 \;\; 1]$$
$$ \Leftrightarrow P = \left[ \begin{array}{cc} \frac{2}{3} & \frac{1}{3} \\ \frac{2}{3} & \frac{1}{3} \end{array} \right] $$
つまり、任意のベクトル \( (x’, y’) \) は、
$$ \left[ \begin{array}{c} \frac{2}{3}x’ + \frac{1}{3}y’ \\ \frac{2}{3}x’ + \frac{1}{3}y’ \end{array} \right] $$
へ移されることになります。確かに \( y = x \) 上にあることが分かります。
本当に任意の \( (x’, y’) \) を \( y = -2 x \) に沿って\( y = x \) へ射影するとこのようになるかどうかは、\( (x’, y’) \) を通り、\( y = -2 x \) に平行な直線
$$ y – y’ = -2 (x – x’) $$
と、 \( y = x \) との交点を求めれば確かめることができます。具体的な計算は記述しませんが、上記と同様の結果が得られることが確認できるはずです。
また、「基底ベクトルのノルムに依存せず射影行列が求まる」という旨を補足として記述していますが、これについては以下のように説明できます。
ある行列 \( A \) の各列ベクトルを左から \( \lambda_{i} (i=1,2,\dots m) \) 倍したとき、それは以下のように表現できる。
$$ [\; \lambda_{1}a_{1} \; \lambda_{2}a_{2} \; \dots \; \lambda_{m}a_{m} \;] = A\Lambda $$
ここで、\( \Lambda = {\rm diag}(\lambda_{1}\; \lambda_{2}\; \dots \; \lambda_{m}) \) と置いています。
射影行列の式において、行列 \( A \) の各列を 定数倍する対角行列を \( \Lambda_{A} \)、行列 \( B \) の各列を 定数倍する対角行列を \( \Lambda_{B} \) と置くと、そのような行列に対する射影行列\( P’ \)の式は、次のように変形できます。
$$ P’ = (A\Lambda_{A})( (B\Lambda_{B})^{T} (A\Lambda_{A}) )^{-1}(B\Lambda_{B})^{T} $$
$$ = A \Lambda_{A} ( \Lambda_{B}B^{T} A\Lambda_{A} )^{-1} \Lambda_{B} B^{T} $$
$$ = A \Lambda_{A}\Lambda_{A}^{-1} (B^{T}A)^{-1} \Lambda_{B}\Lambda_{B}^{-1} B^{T} $$
$$ = A(B^{T}A)^{-1}B^{T} = P $$
行列 \( A \)、\( B \) の各列を定数倍しても、定数倍する前の射影行列と内容が変わらないということが読み取れます。これは、基底ベクトルのノルムによらず、得られる射影行列の表式が同じであるということを意味します。
以上から、基底さえ求めることができれば射影行列を簡単に作れるということが分かりました。
コンピュータグラフィックスなんかで、影を作成するときにこの辺りの知識が役に立つかもしれませんね。
まとめ
この記事では、射影行列 \( P \) がランク落ちしていることの補足説明と、射影先・射影方向が分かっているときの射影行列の作成方法について数式の変形をもとに解説しました。
射影先・射影方向さえわかってしまえば機械的に射影行列を構成できる、という知見は応用上重要な性質かと思います。即座に応用するようなシーンは少ないと思いますが、このような内容を考えることは頭の体操になるので、たまにはじっくり取り組むのも良いと思います。
では今回は以上となります。最後までお読みいただき、ありがとうございました!




コメント