射影行列の定義、意味分からなくね???
こんにちは、novです。
今回は「射影行列」の直感的な理解に焦点を当てて記事を作成してみたいと思います。
射影行列(特に斜交射影行列)について調べると、次のような定義を見かけると思います。
- 正方行列 \( P \) が \( P^2 \) を満たすとき、\( P \) を射影行列という
…何のこっちゃ?と初見の方は思うかと存じます。それもそのはずで、この書き方だと、射影という言葉から連想される
- どこかの軸に影(≒垂線)を落とす
- 実態としての次元が落ちる
といった内容が全く想起されないからです。そこで、この記事ではそのイメージを埋めるために、簡単な数式の変形と、そこから得られるイメージを簡潔にまとめてみようと思います。
射影行列(特に「直交射影行列」とよばれるもの)については、機械学習や最適化において頻出の線形方程式系における「最小二乗解」でよく出てくる式
$$ x^{*} = A(A^{T}A)^{-1}A^{T} b $$
のイメージを掴む上でも非常に重要です(式の中に登場する行列 \(A(A^{T}A)^{-1}A\) が直交射影行列)。
今回の記事を読む上では、行列の積についてちょっとした見方のコツを知っておくとよりスムーズになるかと思います。以下の記事でザックリとですが紹介しているので、そちらも併せてご覧いただければと思います。
射影の基本イメージ
では、射影に関する基本イメージについて紹介します。
基本的には、光源とスクリーンがあるようなイメージです。以下の画像のような感じになりますね。
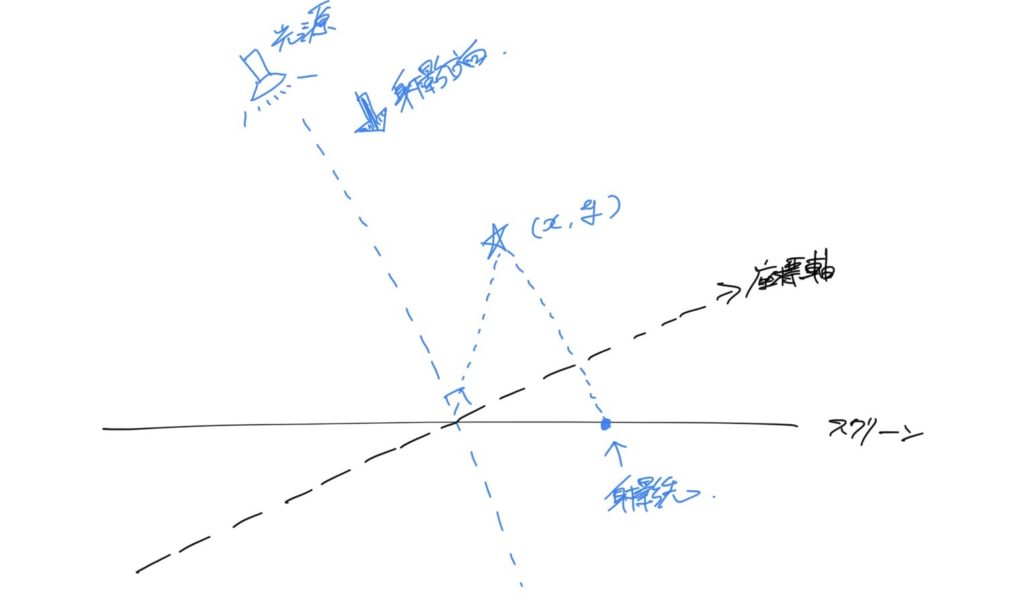
直感が働く範囲ということで、二次元の図を考えています。座標軸に対して斜めにスクリーンがあり、スクリーンと物体を挟んだ反対側に光源がある図ですね。
※ スクリーンと光の向きが直交していないので、正射影ではないことに注意
図を眺めると、この場合に登場する特徴的なベクトルが3つあることに気づきます。
- スクリーン上の位置を表現する、スクリーンに平行なベクトル
- 光の進む方向を表すベクトル
- 光の進行方向と垂直なベクトル(図では座標軸と表現)
スクリーンへの射影を考えるとき、初等的な方法としては
- 光の進行方向と垂直な面への正射影を考え
- その正射影をさらにスクリーンまで伸ばす
という方法が素朴な方法として思いつきそうです。
次章ではこれを図式化し、簡単に計算してみます。
二次元の場合の斜交射影の導出・一般式との比較
早速イメージ画像を載せます。
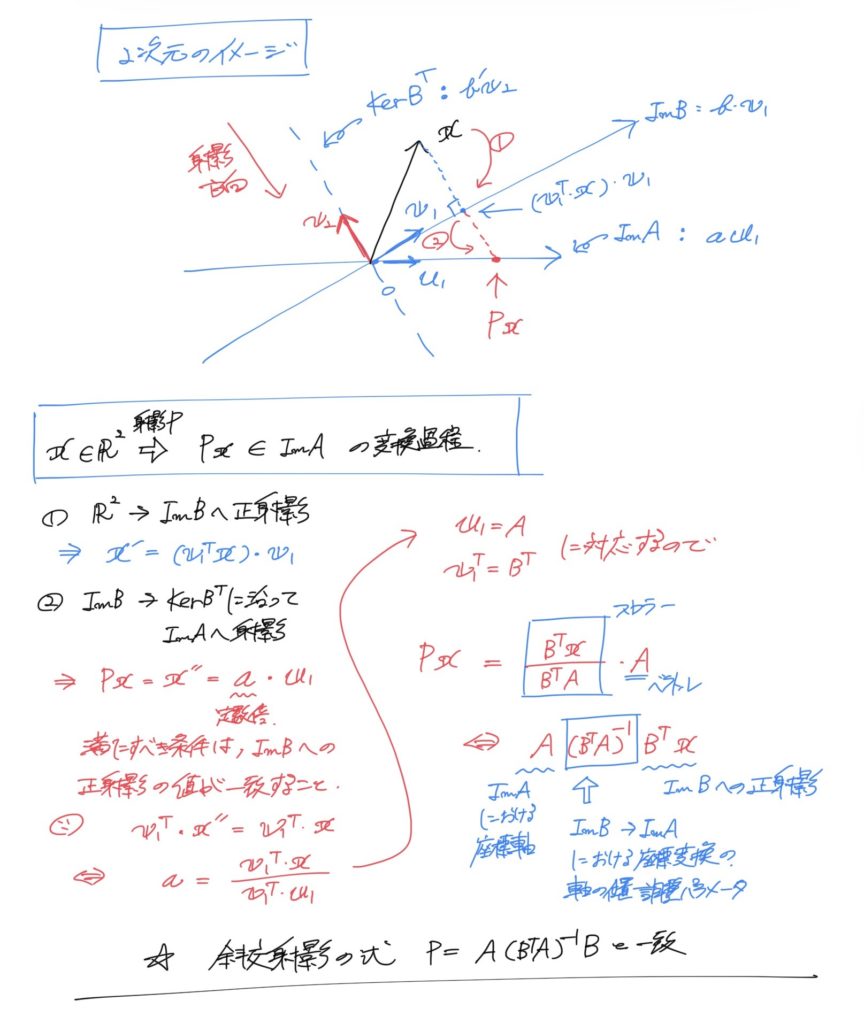
後々の説明の都合上、像空間や核が登場しています。
図の中では、スクリーンに平行なベクトルを\(u_1 = A\) 、光の進行方向に垂直なベクトルを\( v_1 = B \) と表現しています。それぞれのベクトルを定数倍して得られる直線は線形空間を成します。これを図の中では \( {\rm Im} A \)、\( {\rm Im} B \) と表現しています。
また、光の進行方向を表すベクトルについては、\( {\rm Im} B \) と直交補空間を成します。要は、ベクトル\(B\)と直交するということですね。一般に、ある像空間 \( {\rm Im} B \) の直交補空間 \( ({\rm Im} B)^{\perp} \) は、\(B^{T}\) の核 \( {\rm Ker} B^{T} \) に一致するという性質があるので、光の進行方向を表すベクトルは、 \( {\rm Ker} B^{T} \) の要素という捉え方ができます。
言葉の準備を少々しましたが、これらの言葉を使うと、今回考えている射影は
- \( {\rm Ker} B^{T} \) に沿った \( {\rm Im} A \) への射影
と表現することができます。また、\( {\rm Ker} B^{T} \) に沿った \( {\rm Im} A \) への射影 \(P\) については、一般的な表現があり、それは以下のようになります。
$$ P = A(B^{T}A)^{-1} B^{T} $$
これを、二次元で確認しているのが上記の画像の式変形ということになります。ちなみに、この式を二乗すると、もとの値に戻ることが簡単に確認できます。これが冒頭で紹介した \( P^2 = P\) という定義に関わる部分ですね。
さて、図の中にも記載はしているのですが、この式に関しては
- \(B^{T} x\) で任意のベクトル \( x \) を \( {\rm Im} B \) へ正射影
- \( (B^{T}A)^{-1} \) で、\( {\rm Im} A \)、\( {\rm Im} B \) における座標目盛の調整
- 最後の \( A \) は、調整が終わった座標値を、\( {\rm Im} A \)の基底ベクトルに振り分けている
という解釈ができます。斜交射影は二回の変換で表現でき、処理の段階は3段階に分割して考えることができるということですね。
また、上記のイメージがあれば、直交射影が
$$ P = A(A^{T}A)^{-1} A^{T} $$
となることも直感的に理解できることになります。つまり、スクリーンが光の進行方向と垂直に配置されている場合の話であり、\( {\rm Im} A = {\rm Im} B \) が成り立つので、斜交射影の場合の式で \(B\) が \( A \) に置き換わるということですね。
ちなみに、直交射影において、像空間を構成するベクトルが正規直交基底を成すとき、それらを並べて得られる行列 \( A \) は \( A^{T}A = I_{n}\) (=単位行列)となるので、射影行列の式は更に簡単になり
$$ P = AA^{T} = \sum_{i=1}^{n} a_{i} a_{i}^{T} $$
となります( \( a_{i} \) は、\( A \) の列ベクトル )。
この表現からわかることは、「射影先の正規直交基底が与えられたとき、それぞれのベクトルの積で構成される行列を足し合わせればそれが直交射影行列になる」ということです。
複雑な計算をしなくてもサクッと射影行列が求まるのは大きいです。
また、この表式が射影行列を表していることは、任意のベクトルを作用させれば
$$ (\sum_{i=1}^{n} a_{i} a_{i}^{T})x = \sum_{i=1}^{n} (a_{i}^{T}x) a_{i} = \sum_{i=1}^{n} C_{i} a_{i}$$
となることからもすぐ分かります(\(C_{i}\) は定数)。
3次元の場合のイメージ図
あまりきれいな図ではありませんが、3次元の例を考えるとこのようになるというものも用意しているので、参考程度に載せておきます。
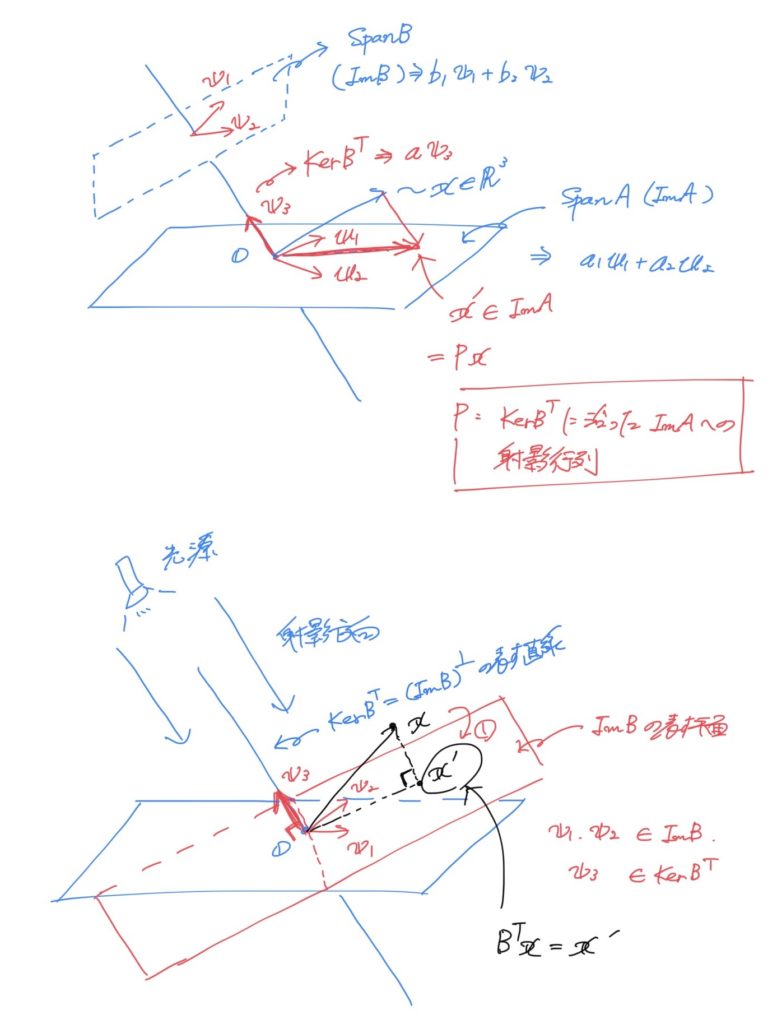
ポイントは、
- 射影先(=スクリーン)を表現する \({\rm Im} A \)
- 光の進行方向を表す \( {\rm Ker} B^{T} \)
- 光に進行方向と垂直な面を表現する \( {\rm B} \)
が登場しており、
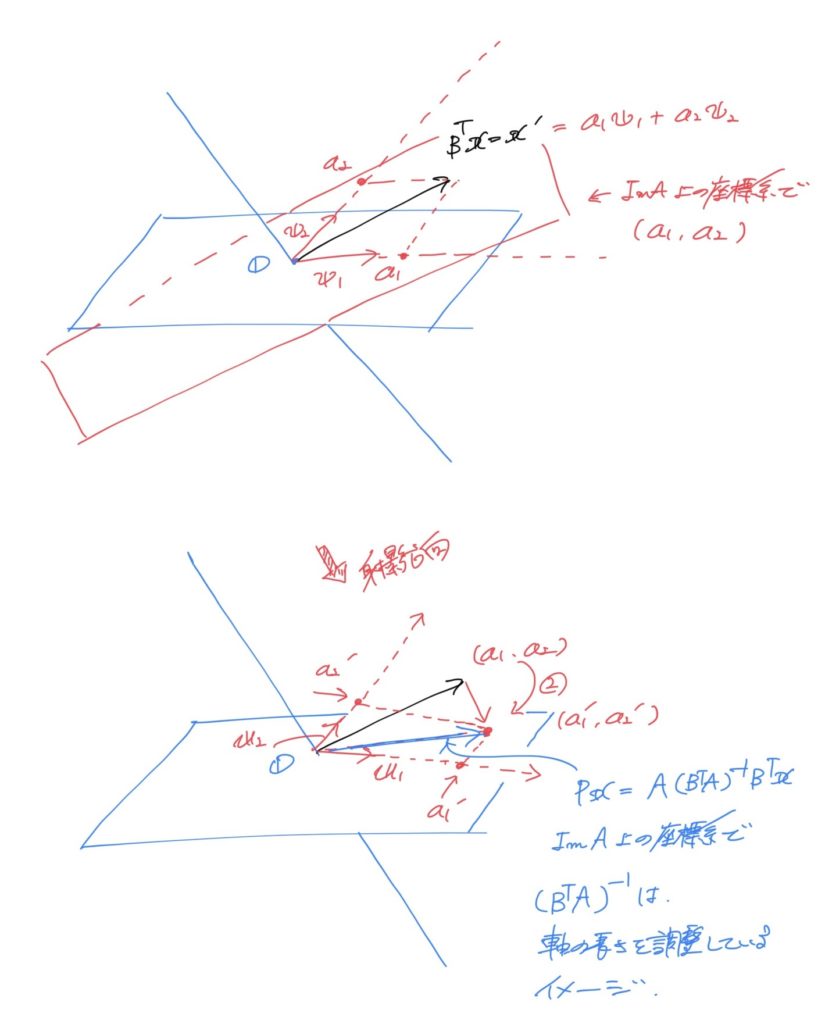
- \(B^{T} x\) で任意のベクトル \( x \) を \( {\rm Im} B \) へ正射影
- \( (B^{T}A)^{-1} \) で、\( {\rm Im} A \)、\( {\rm Im} B \) における座標目盛の調整
- 最後の \( A \) で、調整が終わった座標値を、\( {\rm Im} A \)の基底ベクトルに振り分けている
という操作を行っているということです。計算がめんどくさいので検証はしていませんが、2次元の場合とまったく同様に理解できるはずです。
まとめ
この記事では、射影行列の直感的理解を目標に、2次元空間の例と3次元空間の例を用いてザックリ解説してみました。
厳密な導出に関しては、今回のスコープ外だったので触れていませんが、後日の記事で紹介予定です。今回のイメージがあれば、記号を適宜図に変換することで徐々に理解できるはずです。
ではこの記事は以上となります。最後までお読みいただき、ありがとうございました!




コメント