本記事でやること
先日の記事で、射影行列の直感的な理解と題して図を交えた解説を行いました。
この記事では、このイメージを元にして厳密に射影行列の導出を行ってみようと思います。
具体的にやることは以下の通りです。
- \( P^{2} = P \) の条件から出発して \( P = A(B^{T}A)^{-1}B^{T} \) を導き出す。
これが導出できれば、逆は直ぐに示せます。
つまり\( P^{2} = P \)であることは、\( P = A(B^{T}A)^{-1}B^{T} \) と表現されることの必要十分条件ということですね。
数式の変形だけではイメージが湧きづらいですが、適宜上記の記事で紹介した図を思い浮かべながら読んでいただければと思います。では早速本題に入っていきましょう!
前提とする知識
証明の中で登場する式変形について触れておきます。
- 行列\(B \in {\bf R} ^ {m\times n}\)の像空間を\( {\rm Im} B\)、核を \( {\rm Ker} B\) とするとき、 \( {\rm Ker} B^{T} \) = \( ({\rm Im} B)^{\perp} \)
直感的には「???」という感じですが、以下の流れで理解(証明)できます。
\( {\rm Ker} B^{T} = ({\rm Im} B)^{\perp} \)の証明
集合が一致することの証明なので、以下の二点を示せばOKです。
- \( {\rm Ker} B^{T} \subset ({\rm Im} B)^{\perp} \) ー①
- \( ({\rm Im} B)^{\perp} \subset {\rm Ker} B^{T} \) ー②
① \( {\rm Ker} B^{T} \subset ({\rm Im} B)^{\perp} \) の証明
まず、任意の \( x\in {\rm Ker} B^{T} \) は、\( B^{T}x=0 \)を満たす。
次に、任意の \( y_{1}\in ({\rm Im} B)^{\perp} \) と任意の \( y_{2}\in {\rm Im} B \) に対して、
$$ y_{1}^{T} y_{2} = 0 \tag{1}$$
が成り立つ。 従って、 \( x^{T}y_{2}=0 \)を導ければ、①が示されたことになる。
さて、\( y_{2} = Bv \) (\(v\in {\bf R}^{m}\) ) と表せるので、\( x^{T}y_{2}=0 \) は次のように変形できる。
$$ x^{T}y_{2} = x^{T} Bv = (x^{T} Bv)^{T} = v^{T} (B^{T}x) = 0 $$
二つ目の式変形は、スカラーの転置は等しいことを利用し、最後にゼロと結び付けている部分は\(x\)が\( {\rm Ker} B^{T} \) の要素であることから導いています。これで\( x^{T}y_{2}=0 \)が導かれたので①の証明は終わりです。
② \( ({\rm Im} B)^{\perp} \subset {\rm Ker} B^{T} \) の証明
次は①とは逆の包含関係を示します。具体的には、任意の \( y_{1}\in ({\rm Im} B)^{\perp} \) と任意の \( y_{2}\in {\rm Im} B \) に対して\( y_{1}^{T} y_{2} = 0 \) が成り立つところからスタートし、\( B^{T}y_{1}=0 \) となることを示します。これで②が示せたことになります。
\( y_{2} = Bv \) と表せることから、\( y_{1}^{T} y_{2} = 0 \) は次のように変形できます。
$$ y_{1}^{T}y_{2} = y_{1}^{T} Bv = (y_{1}^{T} Bv)^{T} = v^{T} (B^{T}y_{1}) = 0 $$
ここで、\( v \) は任意の\( y_{2} \) と紐づくベクトルなので、\( {\bf R}^{m} \) 全体を取り得ます。任意のベクトルに対して 内積がゼロになるようなベクトルは零ベクトルのみなので(※背理法で簡単に示せます) 、
$$ B^{T} y_{1} = 0 \tag{2}$$
となります。任意の \( y_{1} \) に対して(2)式が成り立つことが示せたので、②の証明が終わりました。
以上、①・②が示されたので、\( {\rm Ker} B^{T} = ({\rm Im} B)^{\perp} \) が証明されたことになります。
証明を追った後にこの式を再度眺めると、「\(B\)の各列ベクトルと直交する空間と、\( B^{T}x=0 \) となるような \(x\)の集合は等しい」ということを述べていることが分かります。意味としても納得がいきますね。
さて、必要な内容の解説も終わったので、いよいよ本題に入っていきます。
射影行列の導出
導出の概要
射影行列の定義 \( P^{2} = P \) から議論をスタートします。大まかな流れは以下のようになります。
- n次元数ベクトル空間 \( {\bf R}^{n} \) の直和分解が \( {\rm Ker} P \oplus {\rm Im} P\) で与えられる
- \( {\rm Im} P \) の基底を列に並べた行列を\( A \)、\( {\rm Im} P^{T} \) の基底を列に並べた行列を\( B \) と置くと、上記の直和分解が \( {\rm Ker} B^{T} \oplus {\rm Im} A\) と表現できる
- \( {\rm Im} A \) と \( {\rm Ker} B^{T} \) が \( {\bf R}^{n} \) の直和を成すことから、 \( {\rm Ker} B^{T} \) に沿った\( {\rm Im} A \) への射影を考えると \( P = A(B^{T}A)^{-1}B^{T} \) が得られる
唐突に\( A \)、\( B \) が出てきたように感じるかもしれませんが、意味としては
- \( A \):与えられた行列 \( P \) の像空間の基底ベクトル (⇒ 射影先の空間の基底) の集まり
- \( B \):\( {\rm Ker} P\) の直交補空間の基底ベクトルの集まり
となります。2次元の図だと下記のようなイメージですね。
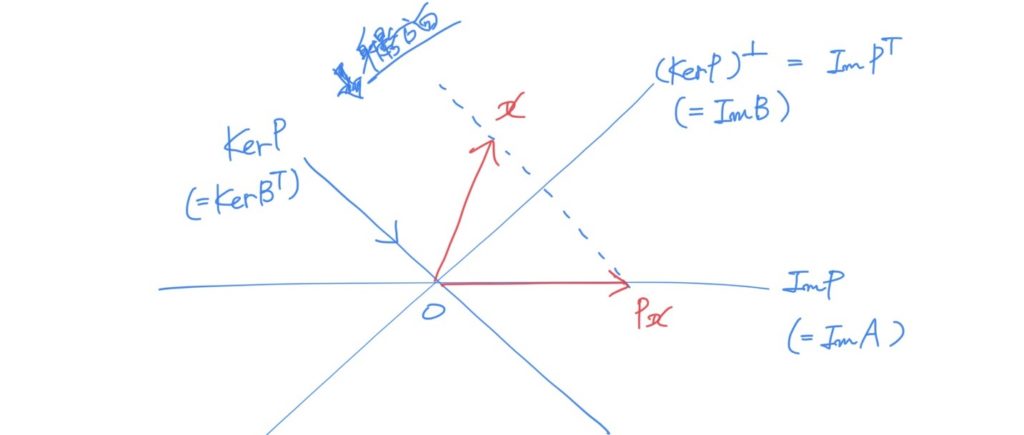
ここまで変形ができたら、あとは \(x\) ⇒ \( {\rm Im} B\) ⇒ \( {\rm Im} A\) と変換する部分を厳密に記述すれば導出が完了することになります。では、概要でリストに挙げた内容を順に示していきましょう。
\( {\bf R}^{n} = {\rm Ker} P \oplus {\rm Im} P\) の証明
これもいくつかのステップで示します。具体的には以下の通りです。
- \( Q=I_{n} – P \) も射影行列となる( \( Q^{2} = Q\) )
- \( PQ =QP = O \)
- \( {\rm Ker} P = {\rm Im} Q \)
- \( {\bf R}^{n} = {\rm Im} P \oplus {\rm Im}Q ={\rm Im} P \oplus {\rm Ker}P\)
以下順番に見ていきます。
\( Q=I_{n} – P \) も射影行列となる( \( Q^{2} = Q\) ) ことの証明
これは単なる式変形で導かれます。使う条件は \( P^{2} = P \) だけです(これしか条件がないので当たり前ですね)。
$$ Q^{2} = (I_{n} – P)(I_{n} – P) = I_{n} – 2P + P^{2} = I_{n} -2P + P = I_{n} – P = Q $$
式変形の通りなので、解説は不要かと思います。
\( PQ =QP = 0 \) となることの証明
これも単なる式変形で導出できます。使う条件も\( P^{2} = P \)だけです。
$$ PQ = P(I_{n}-P) = P – P^{2} = P – P = O $$
$$ QP = (I_{n}-P)P = P – P^{2} = P – P = O $$
これもコメント不要かと思います。
\( {\rm Ker} P = {\rm Im} Q \) であることの証明
前章でやった証明と同じ方法で示します。つまり
- \( {\rm Ker} P \subset {\rm Im} Q \)ー①
- \( {\rm Im} Q \subset {\rm Ker} P \)ー②
の両方を示します。まず、①について見てみましょう。
任意の \( x\in {\rm Ker P} \) に対して、\( Px=0 \)となります。これを変形すると、
$$ x = x + 0 = x + Px = (I_{n} – P)x = Qx \in {\rm Im} Q $$
が成り立ちます。これで①が示されました。次に②について見ていきます。
これについては、 \( PQ = 0 \)を示しているので、任意の \( y\in {\rm Im}Q \) に対して以下の変形で導けます。
$$ Py = PQv = O v = 0 \;\;\; (v\in {\bf R}^{n})$$
これより、\( y \in {\rm Ker} P \) と言えるので、②も示されました。よって\( {\rm Ker} P = {\rm Im} Q \)が言えます。
\( {\bf R}^{n} = {\rm Im} P \oplus {\rm Im}Q ={\rm Im} P \oplus {\rm Ker}P\) の証明
これは、以下のステップで証明します。
- \( {\bf R}^{n} ={\rm Im} P + {\rm Im}Q \) ※ 「+」は和空間を表す
- \( {\rm Im} P \cap {\rm Im}Q = \{0\}\) ⇒ 上記と併せて \( {\bf R}^{n} = {\rm Im} P \oplus {\rm Im}Q\)
- \( {\rm Ker} P = {\rm Im} Q \) より \( {\bf R}^{n} = {\rm Im} P \oplus {\rm Ker}P\)
まず\( {\bf R}^{n} ={\rm Im} P + {\rm Im}Q \)についてです。例によって、以下を示します。
- \( {\bf R}^{n} \subset {\rm Im} P + {\rm Im}Q \)ー①
- \( {\rm Im} P + {\rm Im}Q \subset {\bf R}^{n} \)ー②
まず、①を示します。任意の\( x\in {\bf R}^{n} \) に対して、次のような式変形が成り立ちます。
$$ x = I_{n}x = (P+Q)x = Px + Qx $$
ここで、\( Px\in {\rm Im}P \)、\( Qx \in {\rm Im} Q \) より、右辺の要素は \( {\rm Im}P \) と \( {\rm Im} Q \) の要素の和として表されていることが分かります。すなわち、\( x \) は \( {\rm Im}P \) と \( {\rm Im} Q \) の和空間の要素と言えます。よって、\( {\bf R}^{n} \subset {\rm Im} P + {\rm Im}Q \) が言えて、①が示されました。
次に、②についてですが、\( y_{1} \in {\rm Im}P \)、\( y_{2} \in {\rm Im} Q \) は両方とも \( {\bf R}^{n} \)の要素なので、その和も\( {\bf R}^{n} \)の要素です。したがって②式の\( {\rm Im} P + {\rm Im}Q \subset {\bf R}^{n} \)も成り立っています。
以上、①②が示されたので\( {\bf R}^{n} ={\rm Im} P + {\rm Im}Q \)が成り立つことが言えました。
さて、2番目の式の\( {\rm Im} P \cap {\rm Im}Q = \{0\}\)を示していきます。
任意の \( x\in {\rm Im} P \cap {\rm Im}Q \)を取ると、その\(x\)に対して、ある \( x_{1}, x_{2}\in {\bf R}^{n} \)が存在して、 \( x=Px_{1}=Qx_{2} \)が成り立ちます。要は\( x\in {\rm Im} P \cap {\rm Im}Q \)に対して、射影行列 \(P, Q\)のそれぞれによる射影元が存在するということですね。
さて、この式に左からPをかけると以下のようになります。
$$ P^{2}x_{1} = PQ x_{2} = 0 $$
$$ P^{2}x_{1} = Px_{1}$$
この二つの式と、\( x=Px_{1} \)から、\( x=0 \) が言えます。これは任意の\( x \)からスタートした議論なので、\(x\)は必ず0になります。したがって、\( {\rm Im} P \cap {\rm Im}Q = \{0\}\) ということになります。
\( {\bf R}^{n} \)の部分空間 \(W_{1}, W_{2} \) の和空間は、その交わりが \( \{0\} \) となるとき、直和となるので、この時点で \( {\bf R}^{n} = {\rm Im} P \oplus {\rm Im}Q \) が言えます。
よって、\( {\rm Ker} P = {\rm Im} Q \)から最後の \( {\bf R}^{n} = {\rm Im} P \oplus {\rm Ker}P\) が導かれます。
これでこの部分の証明は終わりです。
\( {\rm Ker} P \oplus {\rm Im} P\) を \( {\rm Ker} B^{T} \oplus {\rm Im} A\) と置くことの説明
この章は、\( {\rm Ker} B^{T} \) に沿った \( {\rm Im}A \) への射影が \( P = A(B^{T}A)^{-1}B^{T} \) と表現されることと、先ほどの議論を繋げるための表現に関する説明です。
証明の概要紹介の部分で、\( {\rm Im} P \) の基底を列に並べた行列を \( A \)、\( {\rm Im} P^{T} \)の基底を列に並べた行列を \( B \)としたときに、この節のタイトルのような表現になることに触れました。
このような置き換えをしている理由なのですが、簡単に言うと射影行列 \( P \) がランク落ちしていることによります。要は\( P \) の列あるいは行のベクトルを並べると、それぞれ線形従属なものが存在するということですね。このとき、\( P \) の像空間 \( {\rm Im} P \) の基底の数は \( n \) よりも小さくなります。
従ってその基底を並べた行列 \( A \) は正方行列ではなくなるということです。そのことを明示するために、\( {\rm Im} P \) の基底の数を \(k (< n)\) 個として、\( A\in {\bf R}^{n \times m} \) と表現しておきます。
このようにすると、\( {\bf R}^{n} = {\rm Im} P \oplus {\rm Ker}P\) が成り立つことより、 \( {\rm Ker}P \) の次元が \( n-k \) であるというように書けます。ここで、前提として紹介した
$$ {\rm Ker} B^{T} = ({\rm Im} B)^{\perp} $$
を応用し、\( B = P^{T} \) と置きなおすと
$$ {\rm Ker} P= ({\rm Im} P^{T})^{\perp} $$
と表せます。\( {\rm Ker} P \) の次元が \( n-k \) であったことと、これが \( {\rm Im} P^{T} \) の直交補空間であることから、\( {\rm Im} P^{T} \) の次元は \( k \) であることが言えます。よって\( {\rm Im} P^{T} \) には基底が \(k\) 個存在することになるので、これらを列に並べた行列を \( B\in {\bf R}^{n\times m} \) とすることで
$$ {\rm Im}P^{T} = {\rm Im} B $$
と表現できます。\( A \) と同様、像空間を正方行列ではない行列で表現しているところがポイントになります。さて、ここまでの内容を、途中で出した図を用いて再度確認してみましょう。

この図は二次元平面におけるある直線方向に沿った射影の図です。この例においては\( P \in {\bf R}^{2\times 2} \)です。さて、図を見ればわかるように、\( {\rm Im}P \) はある直線となるので、その空間の基底はあるベクトル\( a \) となります。これを列ベクトルとした行列が \( A \) になるということですね。要するにこの例では \( A=[a] \)(列ベクトル)ということです。
一方、\( {\rm Ker} P \) も直線であり、その直交補空間も直線になります。\( ({\rm Ker} P)^{\perp} \) は直線ですから、その基底はあるベクトル \( b \) と表現できることになります。これを列に並べた行列が \( B = [b] \)(列ベクトル) ということになります。\( {\rm Ker} P\) の要素は、この \(B\) と直交することになりますので、\( {\rm Ker} B^{T}\) と表現されることになります。最後の部分の証明では、任意のベクトル \( x \) を、\( {\rm Im} B\) へ正射影した後、\( {\rm Im}A \) へと移すことになるので、このイメージを持っておくと理解しやすいかと思います。
※ 文中で \( P \) がランク落ちしているとさらっと述べましたが、これは後日追記するか、別の記事で触れたいと思います。\( P^{2} = P \) という条件だけから導けます。
\( {\rm Ker} B^{T} \) に沿った\( {\rm Im} A \) への射影 \( P\) が \( A(B^{T}A)^{-1}B^{T} \) となることの証明
ではいよいよメインの部分の証明です。基本的な流れは前章で触れたとおりです。
まず、前章のように\( A, B \) を定めているので、\( {\bf R}^{n} = {\rm Ker} B^{T} \oplus {\rm Im} A \) となります。このことから、任意の \( x\in {\bf R}^{n} \) は、ある \( x_{1} \in {\rm Im} A \) と、ある \( x_{2} \in {\rm Ker} B^{T} \) を用いて、 \( x=x_{1} + x_{2} \) と一意に表現できます(直和の定義より)。
\( x_{2} \in {\rm Ker} B^{T} \)より、\( B^{T}x_{2} = 0 \)なので、以下のような変形が成り立ちます。
$$ B^{T} x = B^{T} (x_{1} + x_{2}) = B^{T} x_{1} $$
これは、任意のベクトル \( x \) を、\( {\rm Ker} B^{T} \) に沿って、 \( {\rm Im} B \) へと正射影したことに相当します。
次に、この \( B^{T} x_{1} \) を \( {\rm Ker} B^{T} \) に沿って、\( {\rm Im} A \) へと移すことを考えます。移した先のベクトル\( x_{A} \)を
$$ x_{A} = \sum_{i=1}^{k} v_{i} a_{i} = Av$$
と置きます。なお、\( a_{i} \) は\( {\rm Im} A \) の基底であり、\( v_{i} \) は実数(定数)、\( v \) は \( v_{i} \) を要素に持つ数ベクトルとします。ここで、\( x_{A} \) を \( {\rm Im} B \) へと正射影したものは、上記の \( B^{T} x_{1} \) と一致するはずです(前章で出した図をイメージしてください)。よって、以下の等式が成り立ちます。
$$ B^{T} x_{1} = B^{T} x_{A} = B^{T} A v $$
よって、ここから \( v \) を求めると、以下のようになります。
$$ v = (B^{T}A)^{-1} B^{T} x_{1} $$
ここで、 \( B^{T} A \) は正則なのか(逆行列が存在するのか)?という疑問が出るかもしれません。
実は、\( {\bf R}^{n} = {\rm Ker} B^{T} \oplus {\rm Im} A \) という条件から常に \( B^{T} A \) は正則であることが示せます。これは証明の本質ではないので、補足の章に解説を回します。
さて、 \( v = (B^{T}A)^{-1} B^{T} x_{1} \) が言えたこと、\( B^{T}x_{1} = B^{T} x_{A} \) から \( x_{1} = x_{A} \) となること (※ 背理法で示せます) から、以下が成り立ちます。
$$ x_{1} = x_{A} = A v = A (B^{T}A)^{-1}B^{T} x_{1} $$
従って、 \( P = A (B^{T}A)^{-1}B^{T} \) とおくと、 \( Px_{1} = x_{1} \) が成り立ちます。
また、 \( B^{T} x_{2} = 0 \) より、 \( A (B^{T}A)^{-1}B^{T} x_{2} = 0 \) なので、
$$ A (B^{T}A)^{-1}B^{T} x = A (B^{T}A)^{-1}B^{T} (x_{1} + x_{2}) = A (B^{T}A)^{-1}B^{T} x_{1} = x_{1} $$
となり、\( Px = x_{1}\) ですから、任意の \( x \in {\bf R}^{n}\) は \( {\rm Im} A \) に移されることになります。また、 \( P^{2} \) を考えると、
$$ P^{2} = A (B^{T}A)^{-1} (B^{T} A) (B^{T}A)^{-1}B^{T} = A (B^{T}A)^{-1}B^{T} = P $$
となるので、\( P \) は射影行列の条件を満たしています。
したがって、 \( P = A (B^{T}A)^{-1}B^{T} \) となることが、 \( P^{2} = P \) という条件だけから導かれたことになります。
今回示そうとしていた内容は、以上で終了となります。お疲れさまでした。
【補足】\( B^{T} A \) が正則となることの解説
先ほどの章で説明を飛ばしていた部分の証明になります。
基本的には、 \( B^{T}A \) の固有値がすべて非ゼロであることを示すという方針で進めます。
\( {\bf R}^{n} = {\rm Ker} B^{T} \oplus {\rm Im} A \) という条件が成り立っているので、直和の性質から \( {\rm Ker} B^{T} \cap {\rm Im} A = \{0\} \) と言えます。したがって、非零ベクトルである任意の\( x_{1} \in {\rm Im} A \) については、 \( x_{1} \notin {\rm Ker} B^{T} \) が言えます。これより、任意の非零ベクトル\( v \in {\bf R}^{k}\) に対して、以下が成り立ちます。
$$ B^{T}x_{1} = B^{T}A v \neq 0 $$
つまり、これは固有値を求めるための定義式
$$ B^{T}A v = \lambda v $$
を考えたとき、\( v \) が非零なので \( \lambda \)、すなわち固有値も非零であることを意味します。
\(v\) は任意だったので、\( B^{T}A \) の固有値はすべて非零であると言えます。したがって、\( B^{T} A \) の行列式がゼロにならないので、逆行列が存在します。つまり、\( B^{T}A \) は常に正則と言えます。
まとめ
この記事では、 \( P^{2} = P \) というところを出発点として、斜交射影行列の式
$$ P = A(B^{T}A) B^{T} $$
を実際に導いてみました。一般の次元で成り立つ議論をしたのでやや抽象度が高かったと思いますが、基本的な考え方は以下に集約されると思います。
- 任意のベクトル \( x \) を \( {\rm Ker} B^{T} \) に沿って \( {\rm Im} B \) へ正射影する
- \( Px \in {\rm Im} A\) を、\( {\rm Im} B \) へ正射影し、上記の正射影結果と比較する
- \( A \) は \( {\rm Im} P \) の基底を並べたベクトル
- \( B \) は \( {\rm Ker} P \) の直交補空間の基底を並べたベクトル
とにかく2次元の場合・3次元の場合の図を書いてみるとこれらのやっていることが明確になると思います。こんな感じで、直感的な解釈と厳密な導出をやる記事はちょくちょく書いていこうと思いますので、興味のある方は読んでいただけると嬉しいです♪
では、今回は以上となります。最後までお読みいただき、ありがとうございました!




コメント