行列計算、毎回成分計算するの大変じゃない?
最近流行りの機械学習に入門するとなると、理論面で避けて通れないのが線形代数です。
主に多次元を扱う関係上出てくるのですが、多変数ガウス分布の最尤推定とか、最適化計算とかでも行列を大量に扱う場面というのがしばしば出てきます。
書籍を参考にしていると、成分表示をしていたり突然行列にまとめたりと、解像度が目まぐるしく変わるので、式展開を追いかけるのも一苦労という方、多いと思います。以下はとある日のツイートです(lib-artsさんの引用RTになっています。マズかったら消します…)。
行列演算を「ベクトルを一つの成分と見た時の内積」のように捉えると結構クリアになると個人的には思います。
もちろん合っていることを確かめるには成分計算をするのが一番ですが。。。この考え方ができると、固有値分解も明確に分かりますし、射影行列に関する一歩踏み込んだ理解もできます。 https://t.co/YsKAhSZPhT pic.twitter.com/mttOOwK7oX
— Nov@理論派エンジニア (@Nov_Log893) November 10, 2020
この見方ができるようになると、煩雑な行列の成分計算を、ベクトルの積の組み合わせでとらえることができるようになり、計算イメージを掴むのが比較的容易になります。また、固有値分解の意味や、直行射影行列の表現、行列の低ランク近似がやっていることなどのイメージを掴むのがぐっと楽になります。
ということで、今回はこの行列計算を適切な解像度でとらえるとどうなるのか、式展開とプログラムで計算させた結果を突き合せてイメージを掴むことを目標にします。固有値やら射影行列やらに関してはまた後日別の記事で述べようかなと考えています。では本題に入っていきましょう!
タイトルの主張って結局どういうこと?
要は以下の内容です(画像内に説明も付加しています)。
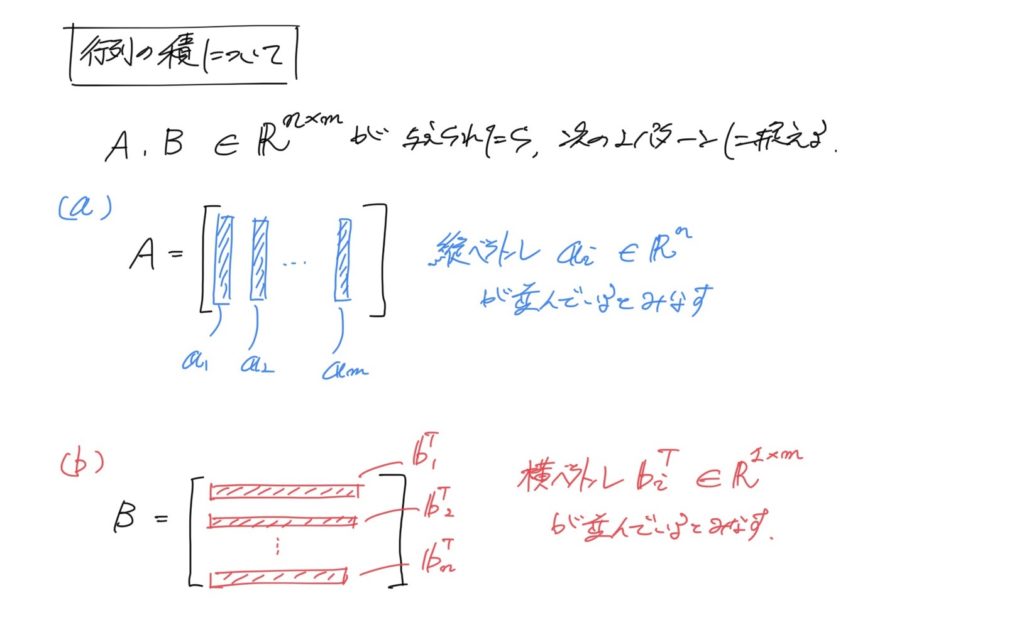
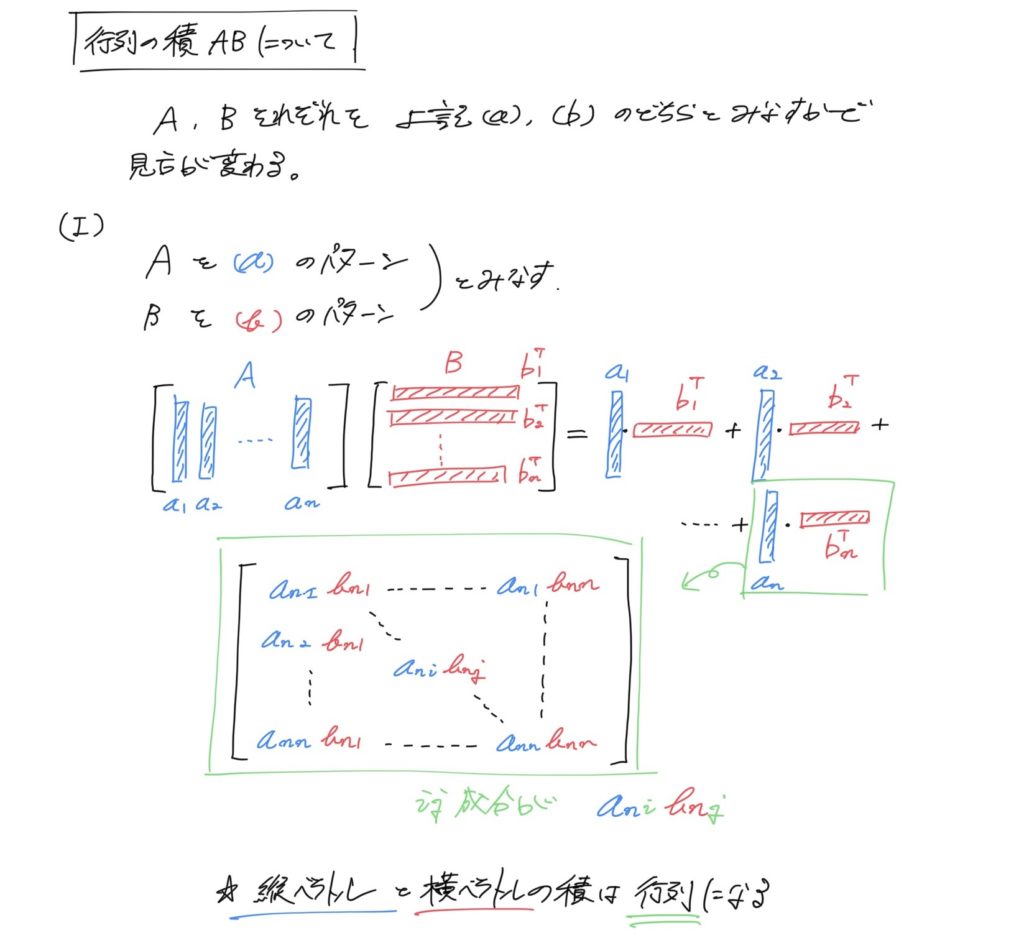
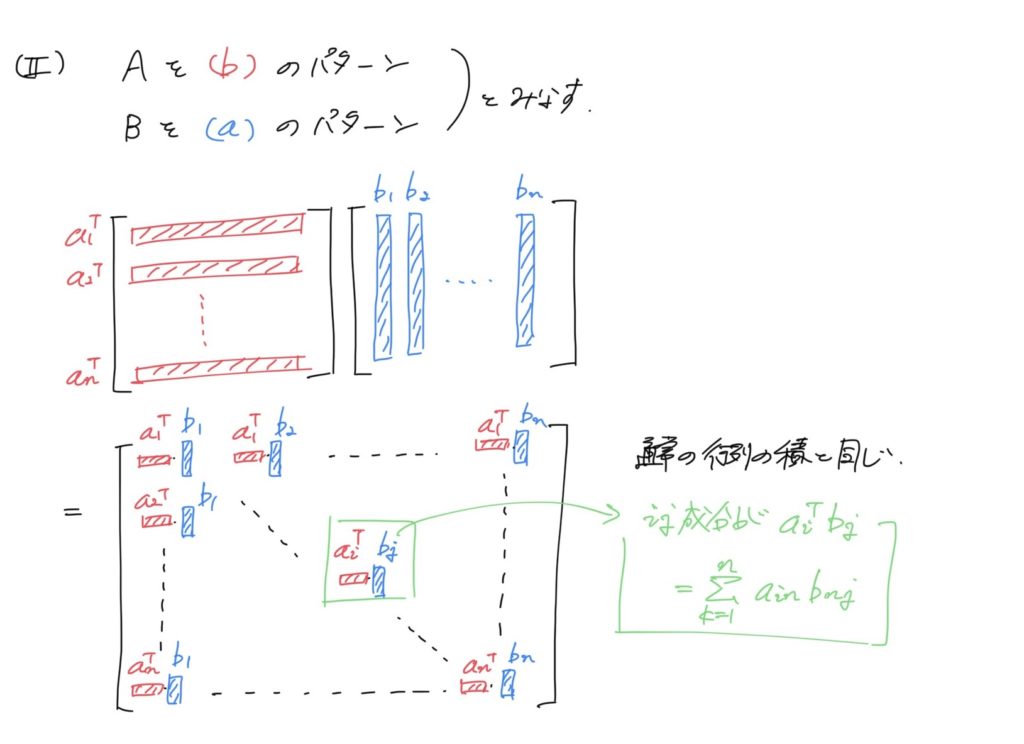
もう少し補足説明すると、
「(II)の見方を普通はするけど、(I)の見方を身に着けると計算が楽になる場合がある」
という主張になります。
具体的には、行列 \(AB\) を何かしらのベクトル \(x\) に作用させた結果を見たい、といったときに、(I)の展開の仕方を知っておくと、計算結果が (スカラー) × \(a_{i}\) の総和になるのが明快に分かるとかといったご利益があります。
この辺は正規直交基底が絡む分野等で特に顕著です(なので固有値分解や直交射影の話、低ランク近似(=次元削減)の文脈で知っておくと有利という話になります)。関連して知っておくと便利な式変形としては以下のようなものもあります。
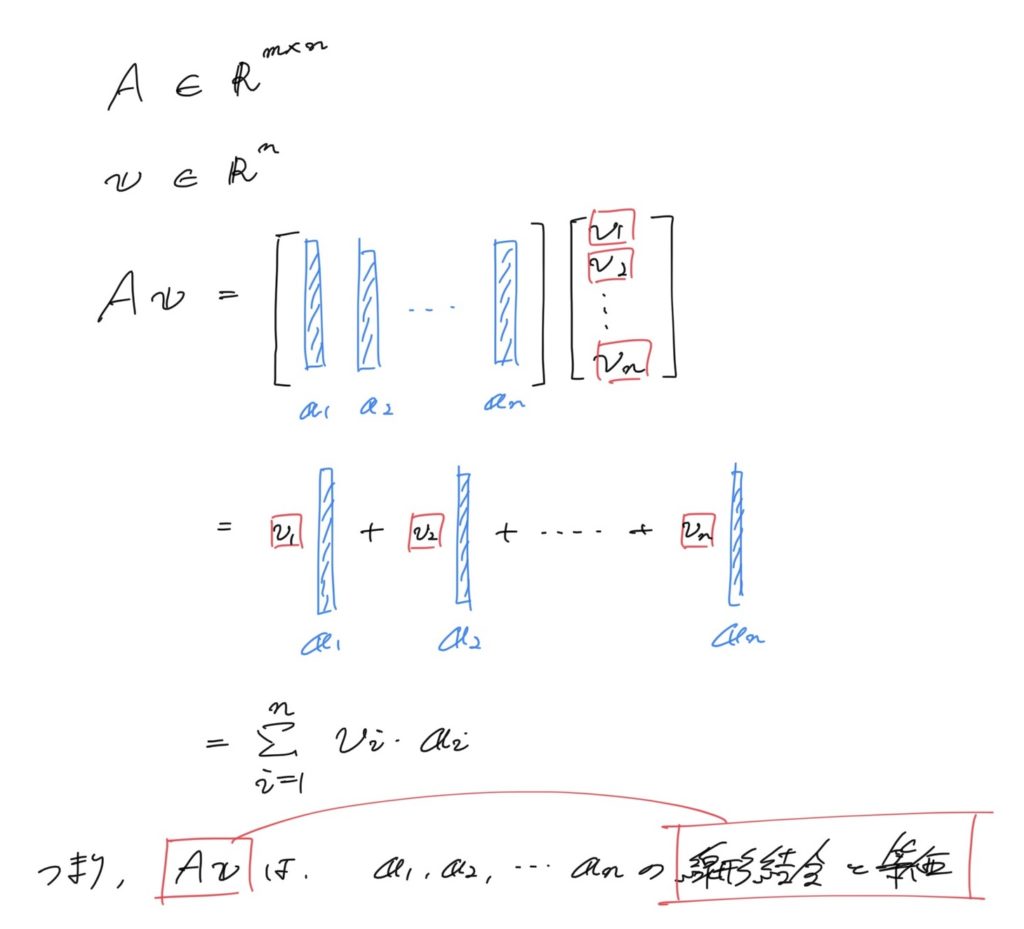
画像の中でも触れていますが、「あるベクトルに行列を作用させること」は「行列の各列に対応するベクトルを線形結合すること」と等価であるとみなすこともできます。この考え方は行列のランクと各列・各行の線形独立性が関わることを理解するうえでも大きな助けになるはずです。
今回は(I)の見方を紹介するという趣旨なので、細かい応用の話は後日書く予定の記事に譲り、実際にサンプルコードで計算の流れを確認してみましょう。
サンプルコードで計算の流れ確認
ではサンプルコードです。簡単のために、3行3列の行列同士の積で検証してみます。
import numpy as np
a = [[1,2,3],
[2,2,2],
[4,3,2]]
b = [[1,1,1],
[3,2,1],
[1,2,3]]
A = np.array(a)
B = np.array(b)
#(II)の計算方法
C = np.zeros((3,3))
for i in range(3):
for j in range(3):
C[i,j] = A[i,:].dot(B[:,j]) # 各要素を内積計算
#(I)の計算方法
D = np.zeros((3,3))
for i in range(3):
ai = A[:,i].reshape(3,1) # 縦ベクトルであることを明示
bi = B[i,:].reshape(1,3) # 横ベクトルであることを明示
D += ai.dot(bi) # 縦ベクトル・横ベクトル = 行列
print("Pattern II")
print(C)
print("Pattern I")
print(D)
"""
【出力結果】
Pattern II
[[10. 11. 12.]
[10. 10. 10.]
[15. 14. 13.]]
Pattern I
[[10. 11. 12.]
[10. 10. 10.]
[15. 14. 13.]]
"""主張したい計算方法が(Ⅰ)の方なので、表示順が逆になっているのはご容赦ください。
内積計算はnumpyのdotで行っています。どのベクトルを掛け合わせているかに着目すると、
- (II) の方(コード上は前者)では、Aの横ベクトル × Bの縦ベクトル
- (I) の方(コード上は後者)では、Aの縦ベクトル × Bの横ベクトル
となっていることが分かるかと思います。dot演算で実際のループが隠れているとはいえ、(I)の方が(II)よりもforのネストが減って、表面上の計算量が減っていることが分かるかと思います。
(もちろん実体としての計算量は両方とも\(O(n^{3}) \)なので注意)
これが何なのかというと、人間が「ベクトルを塊」とみなす限りにおいて、行列演算の見た目の計算量削減に寄与 = 煩雑な手計算から解放されるということを意味します(と個人的に思っています)。
理論的な部分を追いかける際には、こういう詳細な計算が必要ない部分がしばしばあります。そういったときに、このような見方ができると何かと便利です。
まとめ
今回は、行列計算において、その見方を変えると式変形が楽になることがあるという内容について触れ、その計算が通常の行列演算と同じ結果になることをサンプルコードを用いて見てみました。
線形代数における種々の概念は、数ベクトル・行列に関する見方を多数知ることでより理解が深まります(線形代数の本質はさらに抽象化された概念にありますが、それは今のところ置いておきます)。
次回の記事では、この計算方法の応用例として、直交射影行列の表現について触れてみようと思います。今回の記事は短いですが、以上とします。最後までお読みいただき、ありがとうございました!



コメント