この記事では、ディープラーニングで時系列を扱うときに登場する「RNN」の概要について解説してみようと思います。この記事の想定読者は以下の通りです。
- 基本的なニューラルネットワークの知識がある
- RNNについて何となく知っているが、明確なイメージを持っていない人
RNNの勉強を少しやってみたものの、展開する説明が分かりにくくて困っている人(主に昔の自分)に向けて解説を試みます。また、Deep Learningのフレームワークで、RNNのパラメータが良く分からない人にも、その理解の助けとなることを目標にします。
今回は、概要編ということで少々図解をする程度に留めます。詳細は次回以降の記事に記載予定です。
RNNとは何か?
RNNとはRecurrent Neural Networkの略です。ニューラルネットワークにおける隠れ層の出力が、再度入力にフィードバックされた構造をもつものをそう呼びます。以下はよく見かけるタイプの図ですね。(引用元)

言葉で書くとまあそんなものかと感じますが、実際のところどんな構造なのでしょうか?少し検索をかけて出てくるものは簡略化された図が多く、下図のようなニューラルネットの図との結びつきが分かりにくいのではないかと思います(引用元)
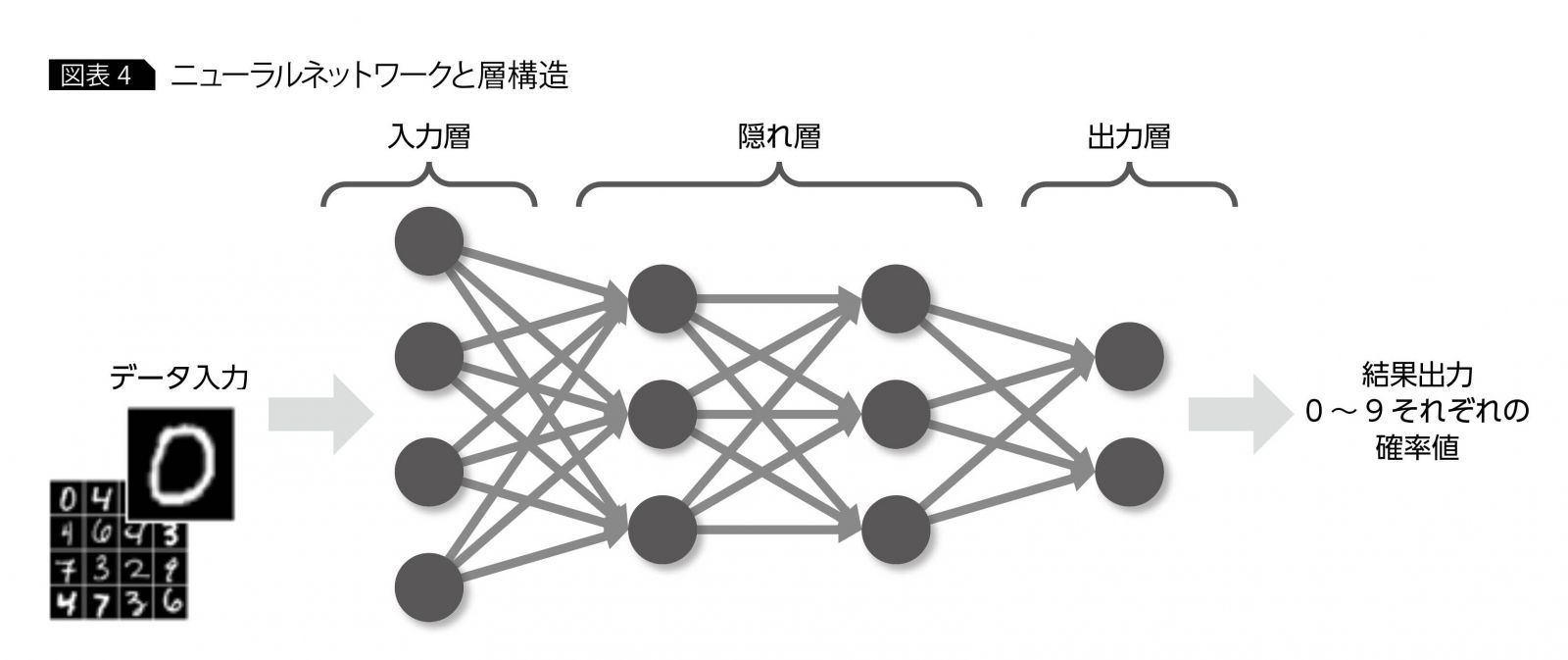
自分も最初にRNNを学んだときは何となくイメージが掴み切れなかったので、初学者向けに細かい部分を補足した資料を作成しようと思った次第です。では、次の章から具体的な構造を見ていきましょう。
RNNの構造
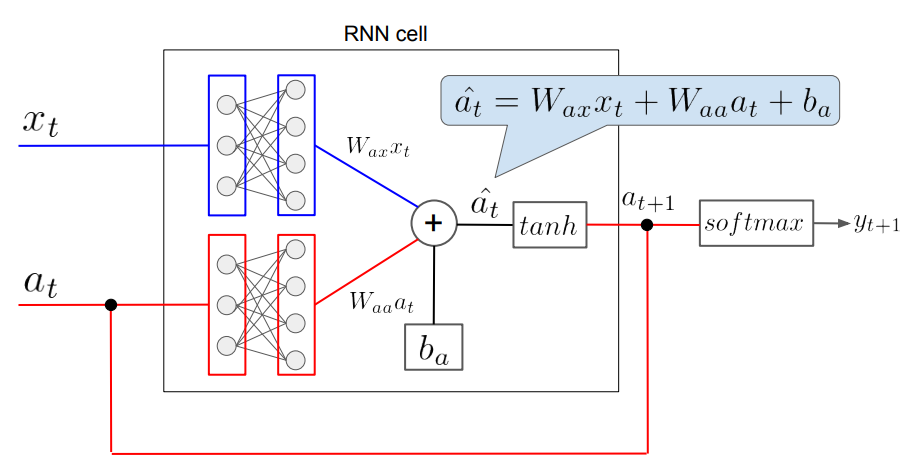
さっそくRNNの構造について見ていきます。以下は、RNNのとある層を模式的に表現したものです。

図中の記号について説明します。
- \(x_t\):時刻\(t\)における入力
- \(a_t\):時刻\(t\)における隠れ層の状態
- \(W_{ax}\):入力を線形変換する行列(RNNのパラメータその1)
- \(W_{aa}\):隠れ層の状態を線形変換する行列(RNNのパラメータその2)
- \(b_a\):バイアス(RNNのパラメータその3)
- \(\hat{a}_t\):時刻\(t\)における、活性化関数(上図ではtanh)を通す前の内部状態
- \(y_{t+1}\):時刻\(t+1\)におけるRNNの出力
通常のニューラルネットワーク(以下NN)では、入力に行列を作用させ、バイアスを付加して活性感関数を通し、最終的な出力が得られます。したがって、パラメータは行列\(W\)とバイアス\(b\)だけということになります。一方、RNNでは隠れ状態\(a_t\)が存在し、それが入力側にフィードバックされているので、パラメータとして行列\(W_{aa}\)が追加されることになります。
これが、構造・パラメータの観点から見た通常のNNとRNNの違いということになります。
RNNの展開(Unfold)
前章までで、基本的なRNNの構造について述べました。次に、RNNの模式図でよく登場する、時間方向への展開図についても触れようと思います。時間方向への展開図とは、以下のようなものです(引用元)。
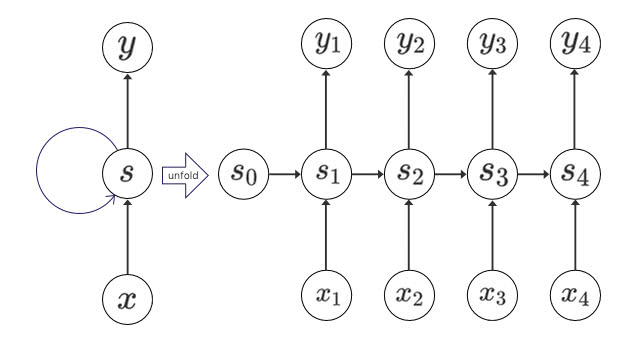
前章の図における「RNN cell」が、この図における”s”と書かれた部分に対応すると考えてください。これも最初に見た時はそんなものかと思うのですが、コードを実装するタイミングでパラメータの扱いなどが曖昧なことに気づきます(ここで引っかかるのは自分だけか?)。そういうわけで、この展開をもう少し詳細に見てみましょう。

スペースの関係で、RNNを展開したもののうち、時刻\(t\)と\(t+1\)の部分だけを抜粋して載せています。図の中にはRNN cellが2つ登場しますが、これらはもともと1つだった層を展開したものなので、パラメータは同一です。ここで注意したいのは、学習時、すなわちパラメータの更新を行うときには同じパラメータは同時に更新されるということです。例えば、パラメータ\(W_{aa}\)について見てみると、これは\(\hat{a}_{t}\)だけでなく\(\hat{a}_{t+1}\)にも影響を与えていることが分かります。すなわち、誤差逆伝播の計算を行うとき、\(W_{aa}\)は\(\hat{a}_{t}\)に関わる項の影響だけでなく、\(\hat{a}_{t+1}\)に関わる項の影響も受けるということです(もちろん、ほかの時刻に関しても同様です)。
これはRNNの誤差逆伝播を考える際に重要なポイントです。これが分かっていればいわゆるBPTT(Back Propagation Through Time)は半分理解したようなものです。また、一つのRNNの層におけるパラメータは\(W_{aa}\)と\(W_{ax}\)と\(b_a\)だけということが分かっていれば、Deep Learningのフレームワークを利用する際に指定するunit数の意味がすんなり理解できるはずです(逆にここが分かっていないと混乱するように思われます)。
まとめ
この記事では、RNNの構造について、図解しながら基本的な部分を概観していきました。機械学習の世界は進歩が早く、時系列データの扱いもRNNではなく”self-attension”という構造にとって代わられる可能性が出てきています。そうである以上、RNNについて学ぶのは今更感もあります。しかしながら、この分野がどのように発展してきたのかという経緯を押さえる上では、RNNをきっちり理解することには意義があると考えます。
次回はRNNの誤差逆伝播の考え方(いわゆるBPTT)について、図を交えながら解説する予定です。数式が多めになるとは思いますが、引き続き読んでいただけると嬉しく思います。それでは。
コメント