この記事では、ディープラーニングの「学習」における重要トピックである「誤差逆伝播法(Back Propagation)」の考え方、数式の導出について記録しようと思います。
※ 自分自身のメモも兼ねているので、間違い・誤植等あるかもしれません。その場合はご指摘いただけると助かります。
目次
誤差逆伝播法とは?
まずはこの記事の中心である「誤差逆伝播法」が何を指すのかを示します。
一言で言うと、「損失関数をDNNのパラメータで微分したときの、微分係数の求め方」です。
まず、DNNと言えば丸(〇)と矢印(→)で構成された以下のような図(グラフ理論における有向グラフ)が思い浮かぶ人が多いと思います(引用元)。
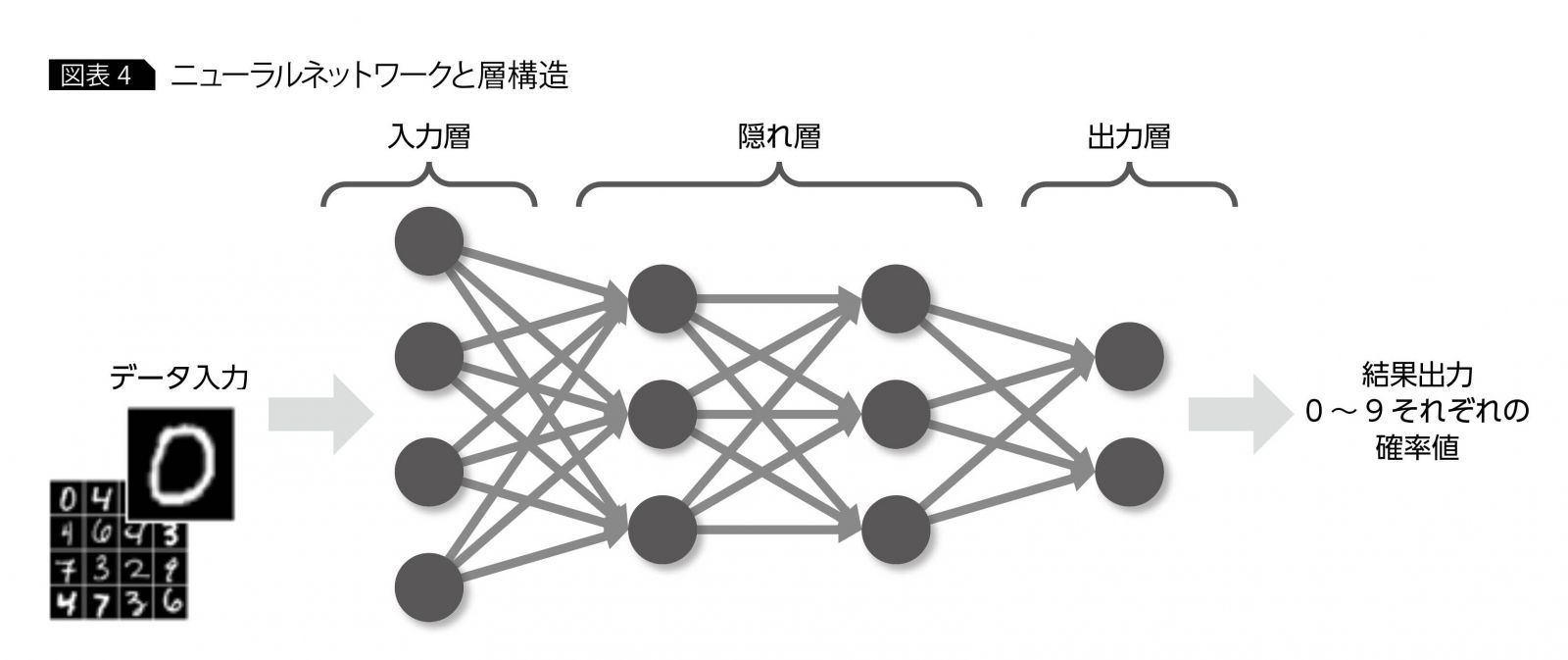
ただ、構造が複雑なだけでDNNも言ってしまえば単なる関数なのです。そして、その関数には多数のパラメータがあり、それを適切に調整することで「ある入力に対する予測値」を出力するようにするというのがDNNの「学習」になります。この「学習」を行う際には、期待する出力と、DNNの出力を比較して「どのくらい予測値がずれているか?」を表す「損失関数」を最小にするようパラメータを決めていきます。
つまり、「DNNの学習」とは「損失関数を最小にするようなパラメータを求める」という問題を解くことと等価です。要は多変数関数を微分して、その微分値がゼロになるようなパラメータを求める問題を解くということですね。
※ 厳密にはKKT条件など、様々な条件を満たさないと微分がゼロでも最適とは限りません
ということで、「誤差逆伝播なんて大層な名前のモノなんか考えず、普通に微分すりゃいいじゃん!」なんて声が聞こえてきそうですが、残念ながらことはそう単純ではありません。
実際に計算をやってみると分かりますが、DNNを表す関数は、多数の非線形関数が何重にも合成されているほか、その一つ一つが多変数関数という非常に厄介な形をしています。ということで、真正面から計算していたら日が暮れる上に、プログラムとして実装することもままなりません。
そこで、合成関数の微分法(=連鎖律)を駆使して、微分計算を漸化式の形で表現するというテクニックが考案されました。これが「誤差逆伝播法」と呼ばれるものになります。
具体的には、以下の一連の式で表現されるようなものです。
【出力層 行列パラメータ】
$$ \frac{\partial E}{\partial V_{pq}} = \sum_{i=1}^{N} \frac{ \partial E }{ \partial \hat{y_{i}} } f’_{ip}(\hat{a}^{(L)}) a_{q}^{(L)} $$
【最終層 内部状態】
$$ \delta_{i}^{(L)} = \sum_{j=1}^{N} \sum_{k=1}^{N} \frac{\partial E}{\partial \hat{y}_{k}} f’_{kj}(a^{(L)}) W_{ji}^{(L)} $$
【第 \( l \) 層 行列パラメータ 】
$$ \frac{\partial E}{\partial W_{pq}^{(l)}} = \sum_{i=1}^{n_{l}} \delta_{i}^{(l)} \phi’^{(l)}_{ip}(\hat{a}^{(l-1)}) a_{q}^{(l-1)} $$
【各層内部状態 漸化式】
$$ \delta_{i}^{(l)} = \sum_{j=1}^{n_{l+1}} \sum_{k=1}^{n_{l+1}} \delta_{j}^{(l+1)} \phi’^{(l+1)}_{jk} W_{ki}^{(l+1)} $$
上記はシンプルなDNNに対してのものなので、DNNの構造によってはまた式が変化します。今回は上記の式を導出することを目標にします。
【この章のまとめ】
- 誤差逆伝播法とは微分計算の1手法
- DNNの学習と微分計算は不可分である
- 真正面から計算していては実装もままならないため、編み出された方法が誤差逆伝播法
ここまでが誤差逆伝播法の導入部分になります。次に、誤差逆伝播法の導出・具体的な計算方法に触れていこうと思います。
誤差逆伝播法の導出【準備】
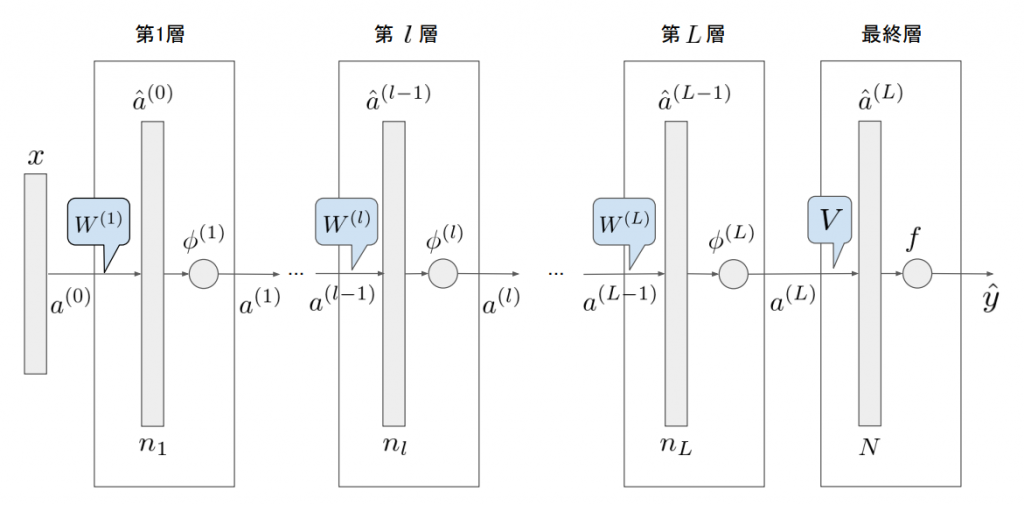
今回の記事では、基本的な考え方を知るためにオーソドックスなDNNの構造を考え、その誤差逆伝播法について考えます。実装することを見越して、ベクトル・行列でまとめた形式で表現することをゴールとします。対象モデルにおいて、隠れ層は全部で\( L \)層あるとします。

まず、図中の記号について説明します。
- \( x \in {\bf R}^{n} \):入力ベクトル(\(n\)次元実ベクトル)
- \( a^{(l)} \in {\bf R}^{n_{l}} \):隠れ層\(l\)の状態ベクトル(\(n_{l}\)次元実ベクトル)
- \( \hat{y} \in {\bf R}^{N} \):出力ベクトル(\(N\)次元実ベクトル)
- \( W^{(l)} \):隠れ層\(l\)のパラメータ行列
- \( V \):出力層直前のパラメータ行列
- \( \phi \):隠れ層の活性化関数(通常はReLUが入る)
- \( f \):出力層の活性化関数(分類問題ならクロスエントロピー、回帰問題ならMSEが多い)
- \(n_{l} \):隠れ層 \(l\) のユニット数(隠れ状態の次元数)
- \( \phi_{l} \):隠れ層 \(l\) の活性化関数
DNNのパラメータとしては、他にバイアス項 \( b \) もありますが、これは隠れ層の状態ベクトルに”1″の成分を付加することで行列パラメータの中に含めることができます。アフィン変換の行列表現を知っている方ならすんなり理解できるはずです。参考となる記事へのリンクも貼っておきます(リンク先)。
次に導出で使う微分関係の定理について触れておきます。
※使いやすい形に変形したものを載せているので、よくある形式とは異なるかもしれません。
【連鎖律】
多変数関数\( f(x_{1}, x_{2}, …, x_{x}) \) の各変数が、共通の変数 \( t \)に依存するとき、
$$ \frac{df}{dt} = \sum_{i=1}^{n} \frac{\partial f}{\partial x_{i}} \frac{dx_{i}}{dt}$$
以下、下付き文字はベクトル・行列の成分を表す添え字とします。では、準備ができたので早速誤差逆伝播法の導出に入ります。
誤差逆伝播法の導出【出力層の行列パラメータ】
まず、損失関数は\(E\) とし、正解データは\(y \in {\bf R}^{N}\)とします。
損失関数\(E\)はDNNによる予測値 \( \hat{y} \)と正解データ \( y \)の誤差を表す関数なので、\(E(\hat{y}, y) \)と表現できます。ここでまず、出力層のパラメータ \(V\)に関する微分を求めます。
パラメータ \(V\)は行列なので、その一成分を取り出して考えます。ここでは代表として\(pq\)成分を考えてみましょう。
$$\frac{\partial E}{\partial V_{pq}} =\sum_{i=1}^{N} \frac{ \partial E }{ \partial \hat{y_{i}} } \frac{\partial \hat{y_{i}}}{ \partial V_{pq} } \tag{1}$$
\(E\)は\( \hat{y} \)のすべての要素に依存しており、\( \hat{y} \)の各要素は パラメータ\(V\)に依存しているため、\(V_{pq}\)にも依存しています。したがって、この記事で紹介している連鎖律が適用でき、式(1)のような式展開になりました。さて、ここで後ろの項 \( \frac{\partial \hat{y_{i}}}{ \partial V_{pq}} \)に着目してみましょう。\( \hat{y_{i}} = f_i(Va^{(L)}) \) ( \(f_i\) は関数 \(f\) の出力の\(i\) 番目の成分)であることから、さらに以下のように展開できます。
$$ \frac{\partial \hat{y_{i}}}{ \partial V_{pq}} = \sum_{j=1}^{N} \frac{\partial f_i(\hat{a}^{(L)})}{\partial \hat{a_{j}}^{(L)}} \frac{\partial \hat{a_{j}}^{(L)}}{\partial V_{pq}} \tag{2}$$
ただし、
$$\hat{a}^{(L)} = Va^{(L)} \tag{3}$$
$$ \hat{a_{j}}^{(L)} = \sum_{k=1}^{n_{L}} V_{jk} a_{k}^{(L)} \tag{4}$$
と置きました。式(2)(4)を見てみると \( \frac{d\hat{a_{j}}^{(L)}}{dV_{pq}} \)の値は、\(j=p, k=q\) のとき以外\(0\)ということが分かります。更に、\(j=p, k=q\) のときは \( a_{q}^{(L)} \)となります。また、式(2)における前の項は、
$$ \frac{\partial f_i(\hat{a}^{(L)})}{\partial \hat{a_{j}}^{(L)}} = f’_{ij}(\hat{a}^{(L)})$$
と表せます。\(f’_{ij}\) は、\(f\) の \(i\) 成分を \( \hat{a}^{(L)} \)の \( j \) 成分で偏微分したことを表します。
したがって、式(1)は次のように書き下すことができます。
$$ \frac{\partial E}{\partial V_{pq}} = a_{q}^{(L)} \sum_{i=1}^{N} \frac{ \partial E }{ \partial \hat{y_{i}} } f’_{ip}(\hat{a}^{(L)}) \tag{5}$$
これでまず、パラメータ\(V\)の微分計算が終わりました。と言いたいところなのですが、プログラムに実装することを見越してこの式をうまくベクトル・行列の形式でまとめられないか検討してみます。
式(5)をよく眺めてみると、総和を取っている部分がベクトルの内積の形になっていることに気づきます。また、添え字\(p, q\)はそれぞれ別々の項についていることが分かります。従って、関数\( f \)のヤコビアンを\( J_{f} \in {\bf R}^{N \times N} \)、損失関数\(E\) のヤコビアンを \(J_{E} \in {\bf R}^{1 \times N}\)として、パラメータ\( V \)による損失関数\( E \)の偏微分は次のように書けます。
$$ \frac{\partial E}{\partial V} = J_{f}^{T} J_{E}^{T} {a^{(L)}}^{T} \tag{6}$$
式(6) は、\(N\times N\)、\(N\times 1\)、\(1 \times n_{L}\)の行列の積になっているので、計算結果は\( N\times n_{L} \)となり、行列\( V \) と同じ形状になっていることが分かります。また、\(pq\)成分を取り出すと、式(5)と一致していることが確認できるかと思います。ちなみにヤコビアンはwikipediaの記事での表現に準拠しています(リンク)。つまり、ヤコビアンの\( ij \) 成分は、関数の第\(i\) 成分を、変数の第 \( j \) 成分で偏微分したものになっているということです。
これでパラメータ\(V\)の偏微分が、行列形式で求まりました。実装の際にも、PythonやMATLABならfor文を陽に書かずに実装できるようになったということです。
以下、同様にして次の微分係数を求めていきます。
$$ \frac{\partial E}{\partial W^{(l)}} $$
$$ \delta^{(l)} =\frac{\partial E}{\partial a^{(l)}} $$
ただし、\( l=1,2,…,L \) とし、そのすべてについて求めることになります。突然出てきた\( \delta^{(l)} \) については、定義しておくと便利なものくらいに考えておいてください。実際、誤差逆伝播法の要である漸化式が\( \delta^{(l)} \)に関して立てられることになります。
誤差逆伝播法の導出【各層の行列パラメータ】
損失関数\( E \) を、今度は \( a_{i}^{(L)} (i=1,2,…,n_{L}) \)に依存すると考えて、\(W_{pq}^{(L)}\) の微分係数を計算してみましょう。すると、次のような式変形ができます。
$$ \frac{\partial E}{\partial W_{pq}^{(L)}} = \sum_{i=1}^{n_{L}} \frac{\partial E}{\partial a_{i}^{(L)}} \frac{\partial a_{i}^{(L)}}{\partial W_{pq}^{(L)}} \tag{7}$$
ここで、式(7)の後ろの項は、前章と同様に、
$$ \frac{\partial a_{i}^{(L)}}{\partial W_{pq}^{(L)}} = \sum_{j=1}^{n_{L}} \frac{\partial a_{i}^{(L)}}{\partial \hat{a}_{j}^{(L-1)}} \frac{\partial \hat{a}_{j}^{(L-1)}}{\partial W_{pq}^{(L)}} \tag{8}$$
となります。式中の \( \hat{a}_{j}^{(L-1)} \)については
$$ \hat{a}_{j}^{(L-1)} = \sum_{k=1}^{n_{L-1}} W_{jk}^{(L)} a_{k}^{(L-1)} $$
と置いてあるので、式(8)については結局 \( j=p, k=q \) の項しか残りません。したがって、以下のようになります。
$$ \frac{\partial a_{i}^{(L)}}{W_{pq}^{(L)}} = \phi’^{(L)}_{ip}(\hat{a}^{(L-1)}) a_{q}^{(L-1)} \tag{9}$$
式(7)および(9)の結果を合わせて
$$ \frac{\partial E}{\partial W_{pq}^{(L)}} = a_{q}^{(L-1)} \sum_{i=1}^{n_{L}} \frac{\partial E}{\partial a_{i}^{(L)}} \phi’^{(L)}_{ip}(\hat{a}^{(L-1)}) \tag{10} $$
となります。なお、式(10) の \( \frac{\partial E}{\partial a_{i}^{(L)}} \) を \( \delta_{i}^{(L)}\)と置くことで、
$$ \frac{\partial E}{\partial W_{pq}^{(L)}} = a_{q}^{(L-1)} \sum_{i=1}^{n_{L}} \delta_{i}^{(L)} \phi’^{(L)}_{ip}(\hat{a}^{(L-1)}) \tag{11} $$
と、簡易的に表現することもできます。また、例によってこの式も行列・ベクトルで表現すると次のようになります。
$$ \frac{\partial E}{\partial W^{(L)}} = J_{\phi_{L}}^{T} {\delta^{(L)}}^{T} {a^{(L-1)}}^{T} \tag{12}$$
\( J_{\phi_{L}} \in {\bf R}^{n_{L}\times {n_{L}}}\) は活性化関数 \( \phi^{(L)} \) のヤコビアンであり、\( \delta^{(L)} \in {\bf R}^{1\times {n_{L}}} \) は損失関数を \( a^{(L)} \) で微分したときのヤコビアンです。式(12) は \( n_{L} \times n_{L}\), \( n_{L} \times 1\), \( 1 \times n_{L-1}\) の行列の積になっているので、計算結果は \( n_{L} \times n_{L-1}\) となり、 \( W^{(L)}\) の形状と一致します。
ほかの層 \(l\) についても、同様の計算を行うことで
$$ \frac{\partial E}{\partial W^{(l)}} = J_{\phi_{l}}^{T} {\delta^{(l)}}^{T} {a^{(l-1)}}^{T} \tag{13}$$
と求めることができます。
ただし、
$$ \delta^{(l)} = \frac{\partial E}{\partial a^{(l)}} $$
です。
さて、これでDNNのパラメータの微分係数は形式上求めることができました。しかし、各 \( \delta^{(l)} \) についてはその微分係数が求まっていません。そこで、以下ではその具体的な式を求めていきます。
誤差逆伝播法の導出【各 \(\delta^{(l)}\)】
この章では、誤差逆伝播法のキモである \( \delta^{(l)} \) の関係式を求めていきます。これが求まれば、導出は完了です。
まず、\( L \) 層について見ていきます。\( \delta^{(L)} \) を定義に従い展開していきます。以下では、その第 \( i \) 成分について計算します。
$$ \delta_{i}^{(L)} = \frac{\partial E}{\partial a_{i}^{(L)}} = \sum_{j=1}^{N} \sum_{k=1}^{N} \frac{\partial E}{\partial \hat{y}_{j}} \frac{\partial \hat{y}_{j}}{\partial \hat{a}_{k}^{(L)}} \frac{\partial \hat{a}_{k}^{(L)}}{\partial a_{i}^{(L)}} $$
まず、最後の項については
$$ \frac{\partial \hat{a}_{k}^{(L)}}{\partial a_{i}^{(L)}} = W_{ki}^{(L)} $$
真ん中の項については
$$ \frac{\partial \hat{y}_{j}}{\partial \hat{a}_{k}^{(L)}} = \frac{\partial}{\partial \hat{a}_{k}^{(L)}} f_{j}(\hat{a}^{(L)}) = f’_{jk}(a^{(L)})$$
なので、次のように表現できます。
$$ \delta_{i}^{(L)} = \sum_{j=1}^{N} \sum_{k=1}^{N} \frac{\partial E}{\partial \hat{y}_{j}} f’_{jk}(a^{(L)}) W_{ki}^{(L)} \tag{14}$$
これも例によってヤコビアン \( J_{f}, J_{E} \)を用いて次のように行列形式の表現が可能です。
$$ \delta^{(L)} = J_{E} J_{f} W^{(L)} \tag{15}$$
この式は、\(1\times N \), \(N\times N\), \( N \times n_{L} \) の行列の積のなので、計算結果は \(1\times n_{L} \) の横ベクトルとなります。
次に、一般の \( l \) について見ていきます。
$$ \delta_{i}^{(l)} = \frac{\partial E}{\partial a_{i}^{(l)}} = \sum_{j=1}^{n_{l+1}} \frac{\partial E}{\partial a_{j}^{(l+1)}} \sum_{k=1}^{n_{l+1}} \frac{\partial a_{j}^{(l+1)}}{\partial \hat{a}_{k}^{(l)}} \frac{\partial \hat{a}_{k}^{(l)}}{\partial a_{i}^{(l)}} \tag{16}$$
最後の項は
$$ \frac{\partial \hat{a}_{k}^{(l)}}{\partial a_{i}^{(l)}} = W_{ki}^{(l+1)} $$
真ん中の項については
$$ \frac{\partial a_{j}^{(l+1}}{\partial \hat{a}_{k}^{(l)}} = \phi’^{(l+1)}_{jk} $$
となります。最初の項は、\(\delta_{}^{(l+1)}\)の定義そのものなので、式(16)は次のようになります。
$$ \delta_{i}^{(l)} = \sum_{j=1}^{n_{l+1}} \sum_{k=1}^{n_{l+1}} \delta_{j}^{(l+1)} \phi’^{(l+1)}_{jk} W_{ki}^{(l+1)} \tag{17} $$
総和の記号が二つ出てきていますが、ReLUなどの活性化関数の場合は \(k\) についての総和はなく、\( k=j \) となることに注意してください。式(17)も行列の積として表現すると次のようになります。
$$ \delta^{(l)} = \delta^{(l+1)} J_{\phi_{l+1}} W^{(l+1)} \tag{18}$$
先ほども触れましたが、活性化関数がReLUなどの場合は、活性化関数に関するヤコビアンが対角行列となるので、もう少し計算量が減ります。ただ、見た目上は式(18)の通りになるということです。
さて、式(18)を眺めると、\( l \) 層の\( \delta \) と \( l+1 \) 層の \(\delta \) に関する漸化式になっていることが分かります。つまり、式(15)で求めた \( L \) 層の \(\delta \) を初項として、1層まで順に\( \delta^{(l)} \) を求めることができるということです。この「最後の層」から「最初の層」まで、誤差が伝わっていくような計算をするため、このアルゴリズムは「誤差逆伝播法」と呼ばれるわけです。
以上、式(15)、(18)と、式(6)、(13)を順次適用することで、DNNのすべてのパラメータに関する微分係数が求まることになります。
まとめ
今回は、通常のDNNの誤差逆伝播法を、微分計算だけで導出しました。単に導出した、というだけなので、これだけでイメージを掴むのは厳しいかもしれません。
次回は、今回導出した計算をDNNの図の中に書き込むとどうなるのか、図解してみようと思います。イメージが掴めるよう努力するので、そちらも読んでいただけると嬉しいです。では今回は以上となります。最後までお読みいただきありがとうございました!

コメント